티스토리 뷰


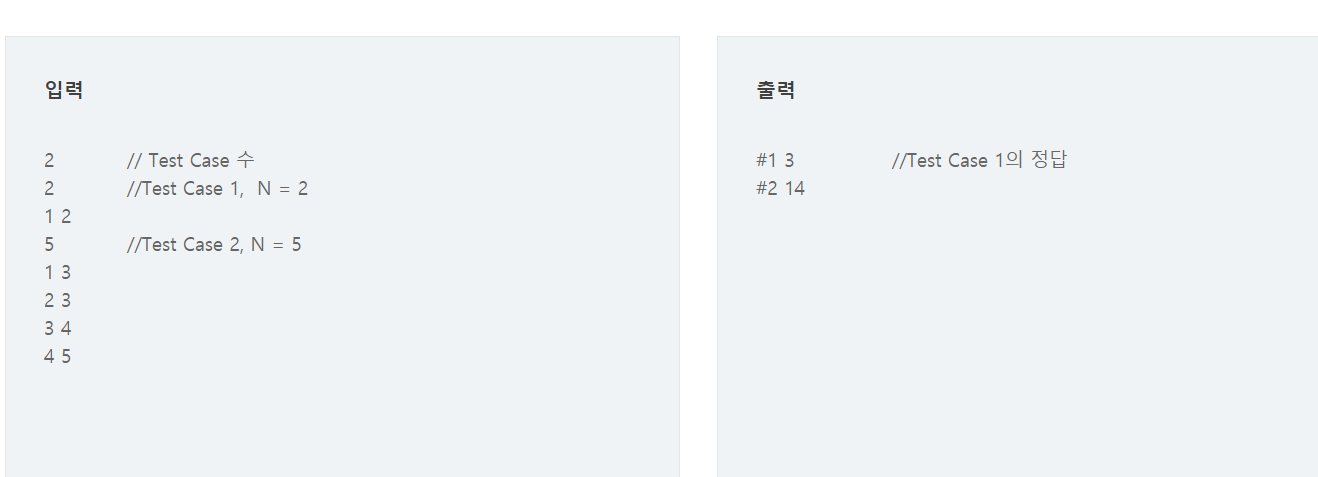
dp를 통해 색칠해 나갈 수 있다
우선 흰색 검은색 가능한데 동시에 연결된 정점이 (검은색/검은색)은 불가능하다
그럼 이 부분만 잘 처리하면 dfs+dp를 통해 해결할 수 있다!
먼저 나의 색을 저장하고 내가 만약 흰색이라면
내 자식들을 (검은색으로 칠하는 경우 + 흰색으로 칠하는 경우)만큼 가능하고
검은색이라면 (흰색으로 칠하는 경우)만 가능하다
경우의 수 이기 때문에 각 자식들의 수의 곱을 구해가면 된다!
long long 조심하자~~
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXN = 1e5+5;
const ll mod=1e9+7LL;
ll d[MAXN][2];
int n;
ll solve(vector<vector<int>>&tree, int pos,int color,int parent){
ll&ret = d[pos][color];
if(ret != -1) return ret;
ret=1;
for(int i=0;i<tree[pos].size();i++){
int next = tree[pos][i];
if(next==parent) continue;
if(!color) ret*=(solve(tree,next,0,pos)+solve(tree,next,1,pos));
else ret*=solve(tree,next,0,pos);
ret%=mod;
}
return ret;
}
int main(){
int t; scanf(" %d",&t);
for(int tc=1;tc<=t;tc++){
memset(d,-1,sizeof(d));
scanf(" %d",&n);
vector<vector<int>> tree(n);
for(int i=0;i<n-1;i++){
int x,y; scanf(" %d %d",&x,&y);
x--;y--;
tree[x].push_back(y);
tree[y].push_back(x);
}
ll ans = solve(tree,0,0,-1)%mod+solve(tree,0,1,-1)%mod;
ans%=mod;
printf("#%d %lld\n",tc,ans);
}
}
|
'알고리즘 > SW Expert Academy' 카테고리의 다른 글
| [SWEA] 1907 모래성 쌓기 (0) | 2020.03.03 |
|---|---|
| [SWEA] 8382 방향전환 (0) | 2020.03.03 |
| [SWEA] 1247 최적경로 (0) | 2020.02.19 |
| [SWEA] 4408 자기 방으로 돌아가기 (0) | 2020.02.11 |
| [SWEA] 1225 암호생성기 (0) | 2020.02.03 |
댓글
