티스토리 뷰


dp로 쉽게 풀 수 있는 문제다
물론 틀렸음~~~!
조건에 맞게 d[x][y][k]로 (x,y)에서 k로 놓는 방법의 수라고 생각해보자
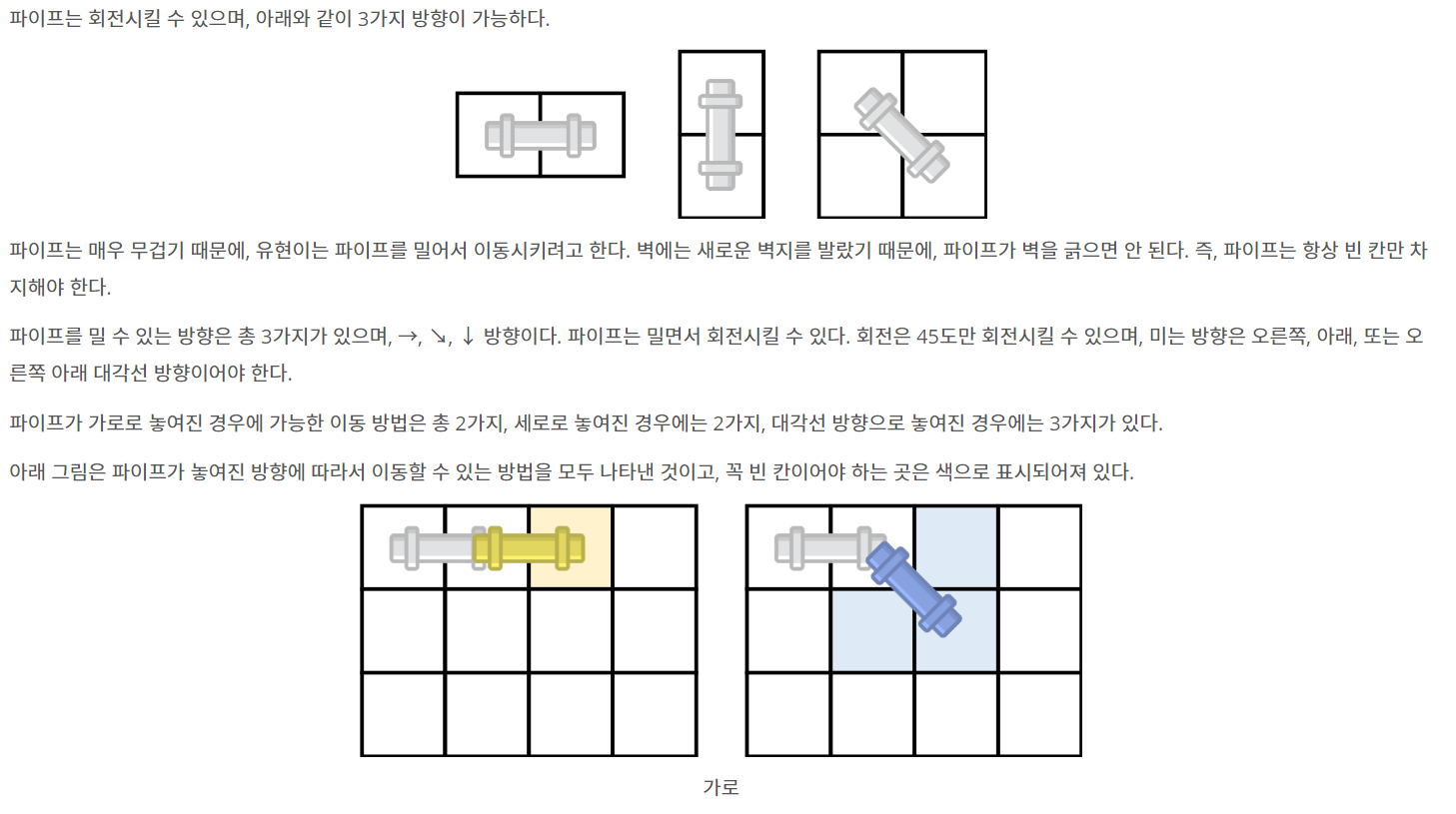
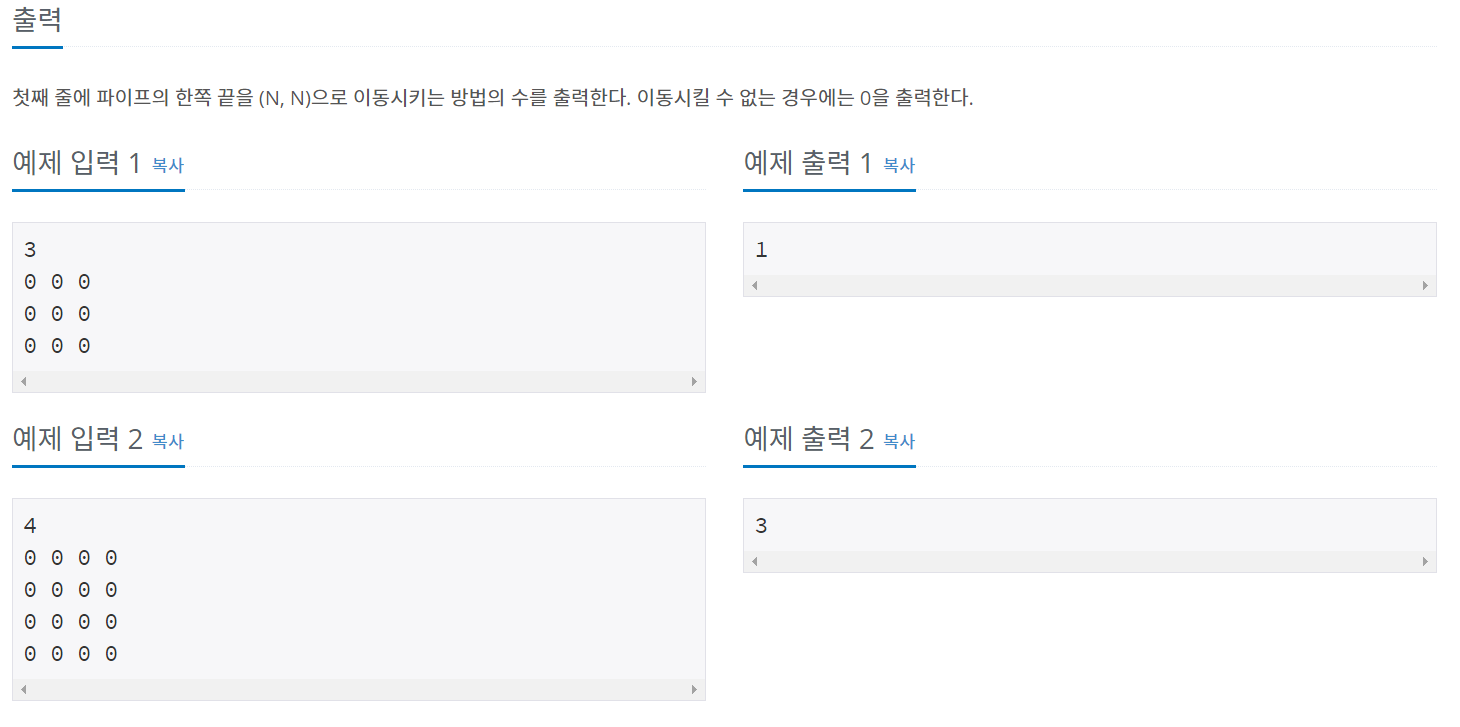
0은 가로 / 1은 대각선 / 2 는 세로다
그럼 내가 가로로 놓기 위해서는
- 현재칸이 0이여야하고
- 다음 칸이 비어있어야하고
- 이전에 가로 or 대각 으로 놓았을 때만 가로로 놓기 가능
따라서 다음 칸이 비어있다면
d[x][y][0] += (d[x][y-1][0] + d[x-1][y-1][1])이 완성된다!
이런 식으로 3방향을 다 보면 된다!
소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
int n;
ll d[33][33][3];
int map[33][33];
bool can(int x,int y){
return (1<=x && x<=n && 1<=y && y<=n && !map[x][y]);
}
int main(){
scanf(" %d",&n);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
scanf(" %d",&map[i][j]);
}
}
d[1][1][0]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(map[i][j]) continue;
int nx = i+1;
int ny = j+1;
if(can(i,ny)) d[i][j][0] +=(d[i][j-1][0]+d[i-1][j-1][1]);
if(can(nx,j)) d[i][j][2] +=(d[i-1][j][2]+d[i-1][j-1][1]);
if(can(nx,ny) && can(i,ny) &&can(nx,j)) d[i][j][1] +=(d[i][j-1][0]+d[i-1][j][2]+d[i-1][j-1][1]);
}
}
ll ans = d[n-1][n-1][1] + d[n-1][n][2] + d[n][n-1][0];
printf("%lld\n",ans);
}
|
'알고리즘 > BOJ' 카테고리의 다른 글
| [백준] 16986 인싸들의 가위바위보 (0) | 2020.02.02 |
|---|---|
| [백준] 1103 게임 (0) | 2020.02.01 |
| [백준] 17135 캐슬 디펜스 (0) | 2020.02.01 |
| [백준] 2526 싸이클 (0) | 2020.01.31 |
| [백준] 14868 문명 (0) | 2020.01.30 |
댓글
